【】〈接上期——〉
六、夹角γ为45°的计算
6.1用基础理论分析图10形式顺时针转动时惯性力
①一阶惯性力的计算
一阶惯性力用表示，下标代表一阶。按照图10从左到右的阅读顺序，其一阶惯性力合力的构成如（7）式所表达
、
坐标系如图所示顺转45°后，变成了气缸对称分布的主方向。一般的，根据坐标系的旋转变换（不是坐标的旋转变换，根据网络百度上发布的信息仔细甄别：坐标的旋转变换是指只有一个坐标系，有一个向量逆时针旋转α后变成一个新的向量，新的点的坐标也可以采用矩阵运算来完成，而其矩阵运算的因子却为，经矩阵的乘法运算后形成新的值还在原来的坐标系中度量，这一点与计算机图学中作“x=x 1”赋值运算一样。可以说坐标的旋转变换与坐标系的旋转变换是一对互为逆运算），有这样的理论：对于标准的直角坐标系即x轴正方向向右，y轴的正方向向上，当xoy坐标系中x轴正方向向着y轴正方向转动时为正值α时，也就是逆时针转动，这时的转换矩阵为，转换矩阵左乘所研究的函数特征，形成了在x'oy'坐标系中新的函数关系式，这不改变该函数的本质属性，但能够帮助人们更清楚认识该函数的图像，不同的视角得出的函数表达式是不相同的，但本质是相同的。因此图（10）是正角45°的坐标系矩阵变换，其因子为
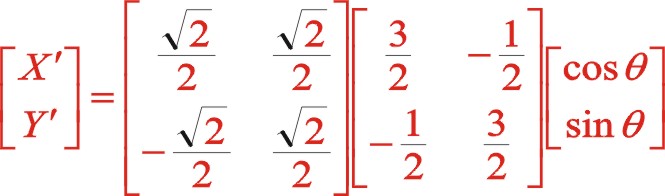
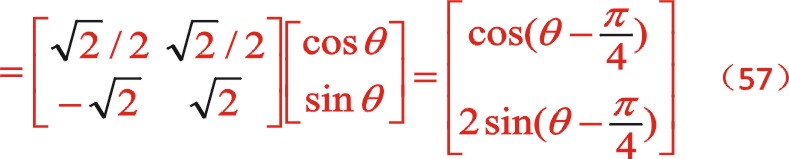
②二阶惯性力的计算
这里先用传统的三角函数来计算。
垂直方向：
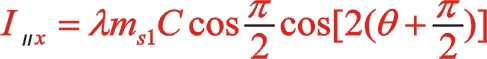
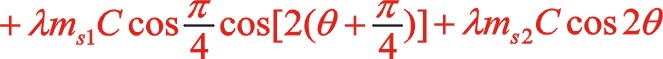
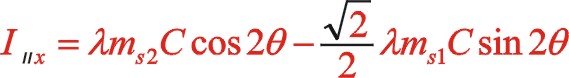
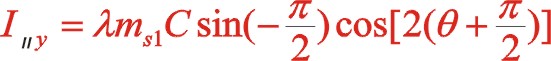
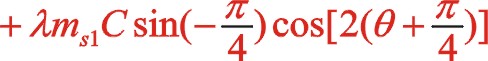
也可以采用复数分析法，下面简单地写出。二阶惯性力用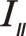
表示，下标ⅱ代表二阶。按照图7从左到右的阅读顺序，其二阶惯性力合力的构成如（11）式所表达
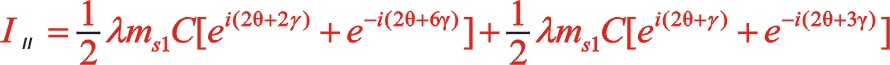
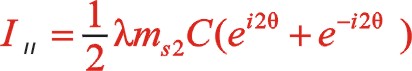
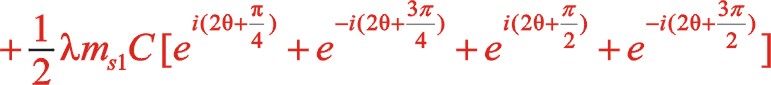
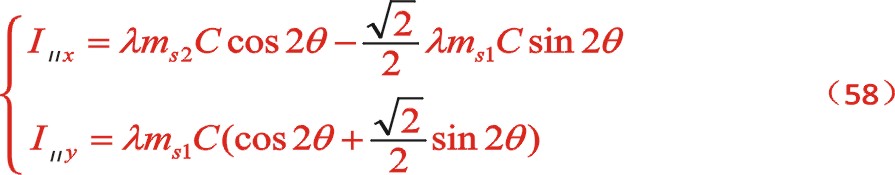
关于w型45°顺转二阶惯性力也有下列的方程运算。
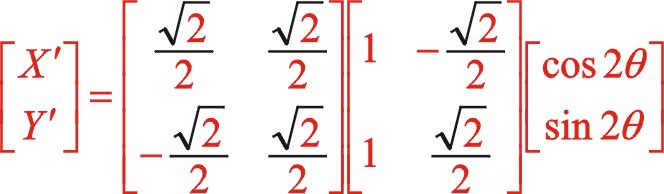
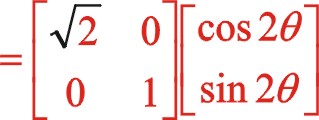
6.2用基础理论分析图11形式反时针转动时惯性力
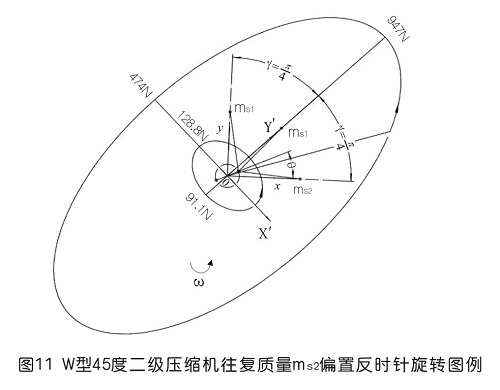
①一阶惯性力的计算
同样，一阶惯性力合力的构成按图11所示的构成，依次写出如下
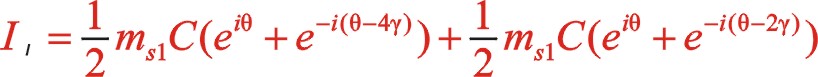
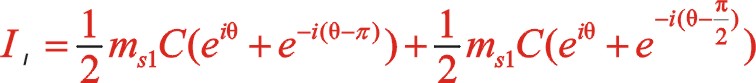
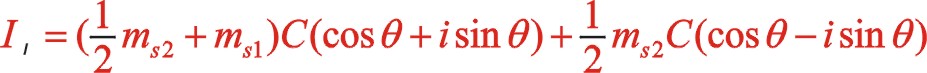
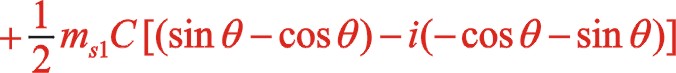
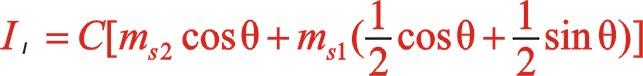
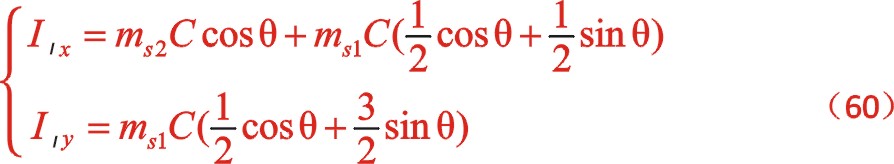
根据上一篇文章75°的文中分析，顺、反旋转时，角度“θ”用“— θ”代替，y方向也就是虚部的代数式“y”用“— y”代替这样的二原则，则式（60）与式（55）比较起来，同样适用这一原则。既适用于一阶，也适用于二阶。60°的情形也同样适用，这里提及一下，有兴趣的读者可以回看一下。
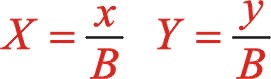
坐标系作负值45°变换，则
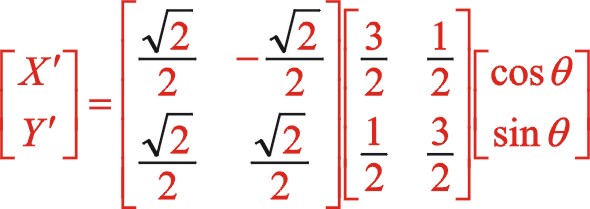
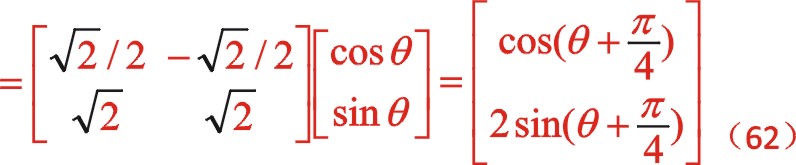
②二阶惯性力的计算
二阶惯性力合力的构成按图11所示的构成，依次写出如下
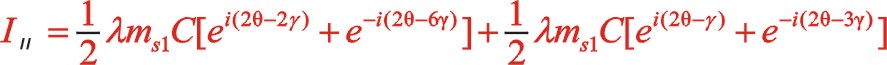
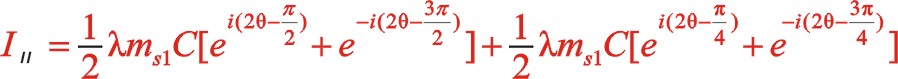
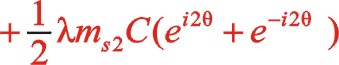
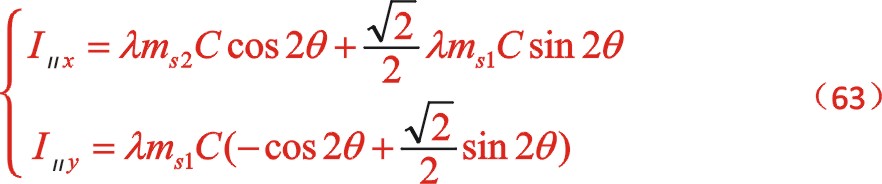
由上一篇文章75°的文中分析，顺反旋转时，角度“θ”用“— θ”代替，y方向也就是虚部的代数式“y”用“— y”代替这样的二原则，则式（63）与式（58）比较起来，同样适用这一原则。这可以检验运算过程的正确性，或者可能由于误输入加减符号导致的常识性错误。60°的二阶惯性力表达式也遵循这个，有兴趣的读者可以回看一下。
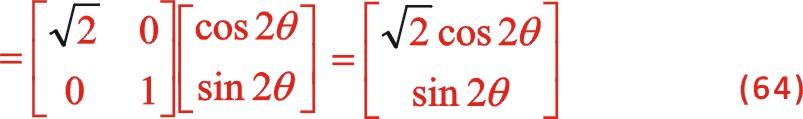
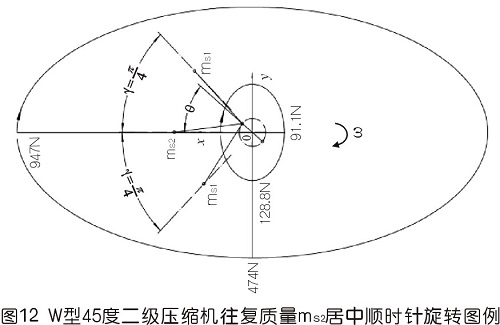
6.3用基础理论分析图12形式顺时针转动时惯性力
①一阶惯性力的计算
一阶惯性力合力的构成按图12所示的构成，依次写出如下
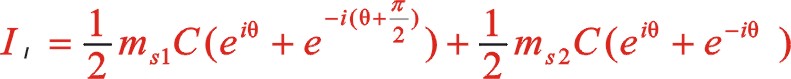
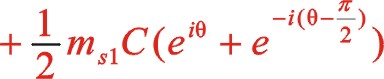
若两质量相等，则可以得出w型45°上述三种情形一阶惯性力的椭圆的短长轴之比为0.5。
②二阶惯性力的计算
二阶惯性力合力的构成按图12所示的构成，依次写出如下
垂直方向：
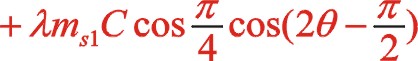
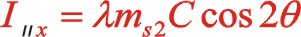
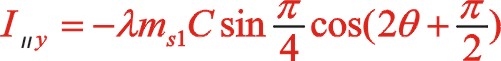
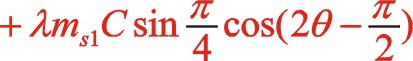
根据式（66），若两质量相等，可得出w型45°上述三种情形二阶惯性力的椭圆的短长轴之比为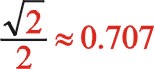
。
6.4图12与图10、图11利用坐标系旋转变换作出的公式的一致性推导
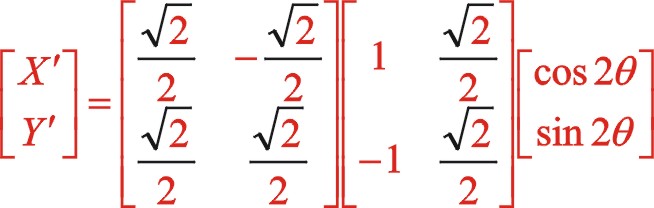
根据前述的理论，我们将图12的坐标系顺旋转方向转动45°后建立了新坐标系，也就是正角变换，这样一来该坐标系就与图10中一模一样。我们所做的事是已知式（65）的方程，利用该式怎样推导出式（56），以验算理论推导过程的一致性。我们进行坐标系的旋转变换，作如下
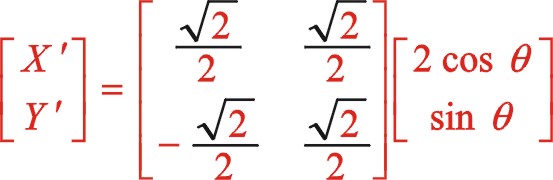
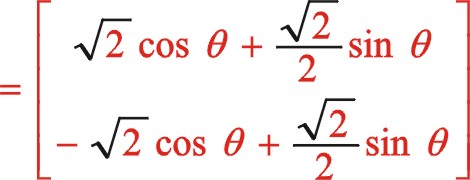
因为我们得到的式（56）是从偏置时开始计角度的，设重新建立新的坐标系后我们从偏置一边的活塞时开始计及角度α，则上面的“θ”用“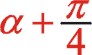 
”来代替，经运算后
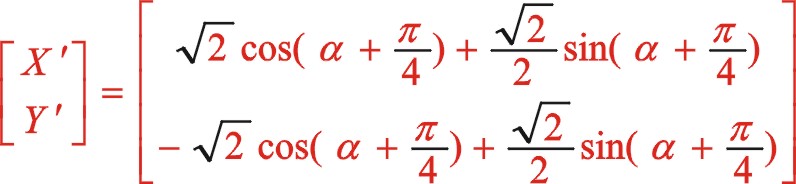
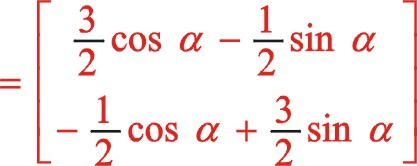
上式与式（56）一样，所以得证。
由于图12所画的转向是顺时针，为弄明白坐标系的旋转变换是正角变换还是负值变换，可以作图11的镜像图，所以得到是负角变换，因镜像后两图转向已一致所以式（65）保持不变，考虑到新坐标系的开始角的度量关系所以“θ”用“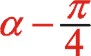 
”来代替，推导如下：
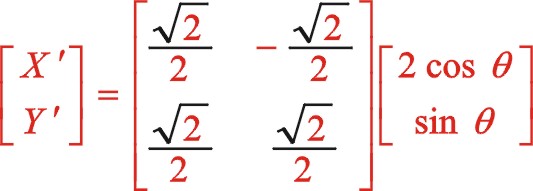
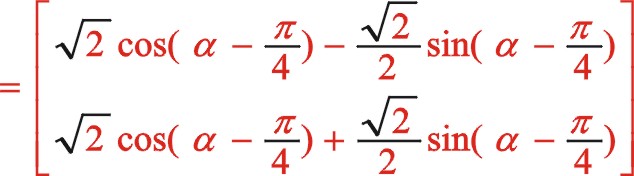
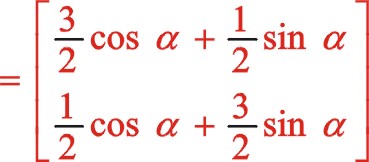
该式与式（61）保持一致，得证。
二阶惯性力的代数式（66）、（58）、（63）也能进行一致性推导。其它角度也行，此处不展开读者如若有兴趣自行推导。下面简单写出该角度的二阶惯性力推导方程式
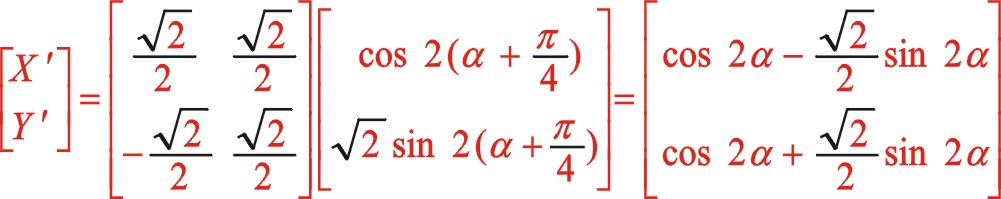
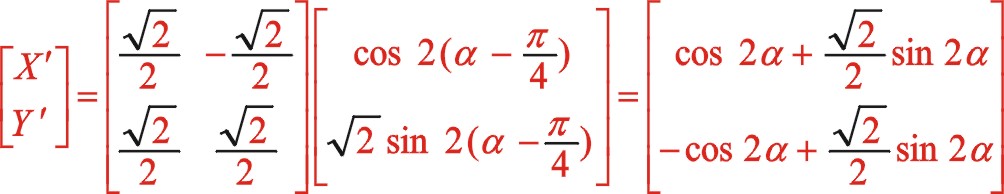
这种通过居中布置的参数方程推导出偏置时的参数方程，仅适用于ms2＝ms1时，对于二者质量不相等的情形，不能够通过坐标系的旋转变换来推导，因为研究的方法可灵活而固有的结构ms2不能够旋转，更多的理论——椭圆的小偏转理论、60°分布时椭圆大旋转理论——似乎也能支持该种算法。因此，还是用传统的方法计算各自的方程来得更直接些。
进行这些运算，可以加强理论的缜密性，可以检验推导过程的正确性，这些都是基于对数学中线性代数学科的研究、基于平时的善于发现，基于前述的基础理论中的正方向理论。
6.5总结
本处以安徽华晶机械有限公司生产的ww-0.9/10b-q型全无油二级为模版，假定气缸夹角为45°，计算其一、二阶往复惯性力。此处先假定三列往复质量相等，即ms为1.8kg，曲柄半径为0.0375m，曲柄半径连杆比λ为37.5/195，角速度ω为2π×(800/60)rad/s，现将上述结构参数分别代入上文中所列的相关公式中，运用计算机内excel程序列表、绘图计算分析，计算的结果绘制在上图的图10、图11、图12中，可以得到以下结论：
1）一阶惯性力由60°分布的圆变成椭圆，且椭圆的短长轴之比由1变成0.5，如果方向一致则是由1变成2；平均值由711n变成731n，有所增大；方向由跟随变成近似跟随。图10、11中已画出一、二阶惯性力刚开始时的矢量线，用椭圆断开表示，图12中反映一阶惯性力在某个时候有重合的可能。
2）二阶惯性力说明，其椭圆短长轴之比由0.333变成0.707。力的平均值由96.9n变成110.8n，有所增加。方向初看是乱的，但很有规律，因为三角函数是周期函数。这个规律待人们去认识、研究、发现、找寻合适的机构来平衡。
3）当ms2≠ms1时，60°分布一阶惯性力在ms2列方向形成椭圆的对称轴，而45°不是，说明角度优先于质量，说明w型时，60°分布是最优的。从式（9）的复数表达式、式（10）的几何表达式中可以看出，60°分布时一阶惯性力长短轴与角度无关，仅与质量有关，这与上也是吻合的。
4）它们的共同点是，曲柄转1周，一阶惯性力也转1周，且同向；二阶惯性力转2周，也同向。
若ms2≠ms1，会引起图10、图11、图12中两个椭圆有所歧化，或偏转，兼带扩压，使其相位、幅值有微量变化。
〈注：本文未完待续，更多精彩见下期！〉
参考文献
（1）宋瑞林，气缸夹角为60°的v6车用往复惯性力的平衡分析，[j]，汽车技术，1988.8
（2）李松虎，3w型往复惯性力的分析，[j]，压缩机技术，1987.3
（3）陆鹏程，张光胜，三星型压缩机振动问题研究，[j]，安徽工程科技学院学报，2009.1
（4）王再顺，夹角为90°的v型压缩机往复惯性力平衡的探讨，[j]，压缩机技术，1986.2
作者简介
陆鹏程，男，安徽桐城人，海军工程大学在职硕士毕业。现在中国人民解放军第四八一二工厂，安徽华晶机械有限公司工作，高级工程师。研究方向：压缩机研究与强度设计。
来源：本站原创
【】〈接上期——〉
六、夹角γ为45°的计算
6.1用基础理论分析图10形式顺时针转动时惯性力
①一阶惯性力的计算
一阶惯性力用表示，下标代表一阶。按照图10从左到右的阅读顺序，其一阶惯性力合力的构成如（7）式所表达
、
坐标系如图所示顺转45°后，变成了气缸对称分布的主方向。一般的，根据坐标系的旋转变换（不是坐标的旋转变换，根据网络百度上发布的信息仔细甄别：坐标的旋转变换是指只有一个坐标系，有一个向量逆时针旋转α后变成一个新的向量，新的点的坐标也可以采用矩阵运算来完成，而其矩阵运算的因子却为，经矩阵的乘法运算后形成新的值还在原来的坐标系中度量，这一点与计算机图学中作“x=x 1”赋值运算一样。可以说坐标的旋转变换与坐标系的旋转变换是一对互为逆运算），有这样的理论：对于标准的直角坐标系即x轴正方向向右，y轴的正方向向上，当xoy坐标系中x轴正方向向着y轴正方向转动时为正值α时，也就是逆时针转动，这时的转换矩阵为，转换矩阵左乘所研究的函数特征，形成了在x'oy'坐标系中新的函数关系式，这不改变该函数的本质属性，但能够帮助人们更清楚认识该函数的图像，不同的视角得出的函数表达式是不相同的，但本质是相同的。因此图（10）是正角45°的坐标系矩阵变换，其因子为
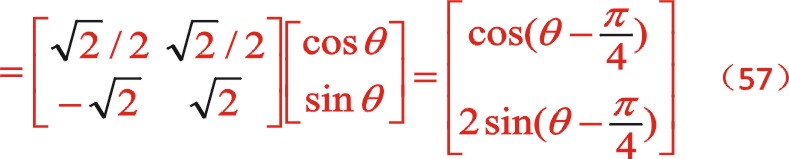
②二阶惯性力的计算
这里先用传统的三角函数来计算。
垂直方向：
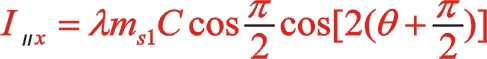
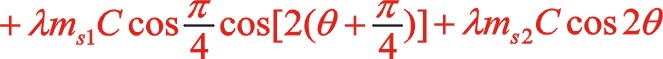
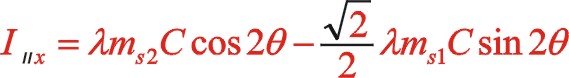
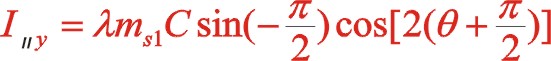
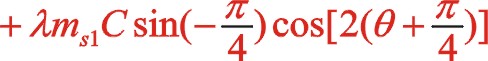
也可以采用复数分析法，下面简单地写出。二阶惯性力用表示，下标ⅱ代表二阶。按照图7从左到右的阅读顺序，其二阶惯性力合力的构成如（11）式所表达
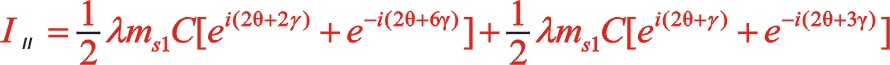
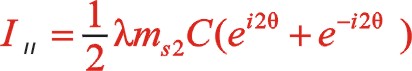
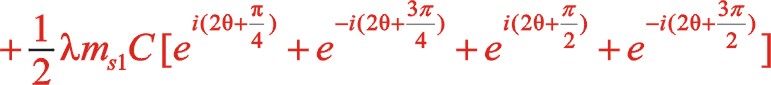
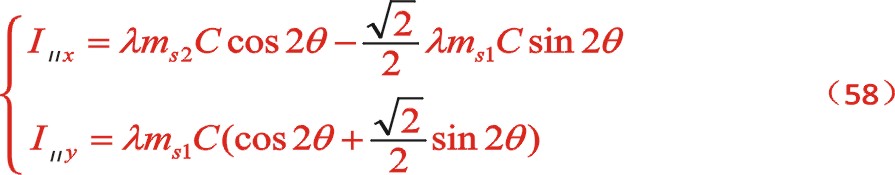
关于w型45°顺转二阶惯性力也有下列的方程运算。
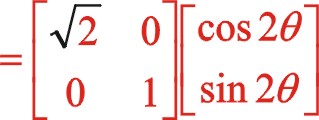
6.2用基础理论分析图11形式反时针转动时惯性力
①一阶惯性力的计算
同样，一阶惯性力合力的构成按图11所示的构成，依次写出如下
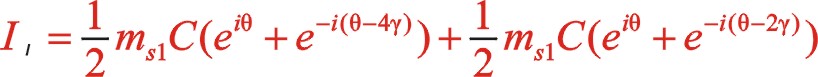
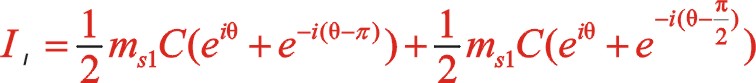
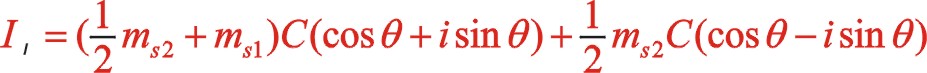
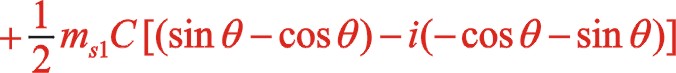
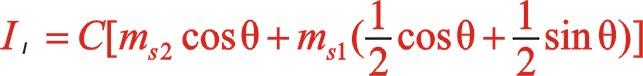
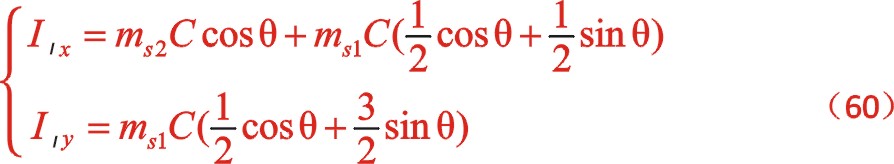
根据上一篇文章75°的文中分析，顺、反旋转时，角度“θ”用“— θ”代替，y方向也就是虚部的代数式“y”用“— y”代替这样的二原则，则式（60）与式（55）比较起来，同样适用这一原则。既适用于一阶，也适用于二阶。60°的情形也同样适用，这里提及一下，有兴趣的读者可以回看一下。
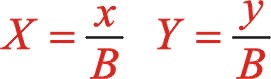
坐标系作负值45°变换，则
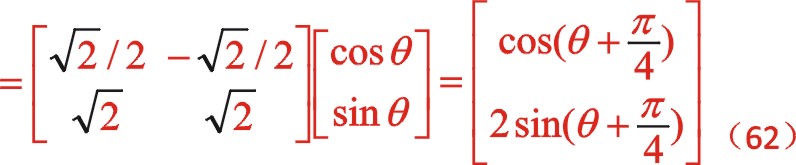
②二阶惯性力的计算
二阶惯性力合力的构成按图11所示的构成，依次写出如下
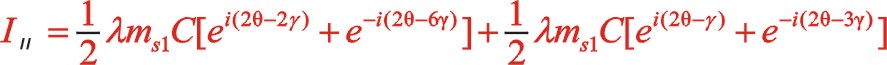
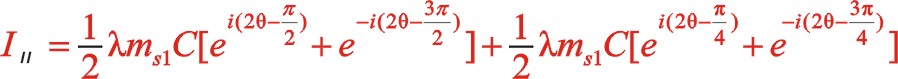
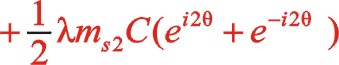
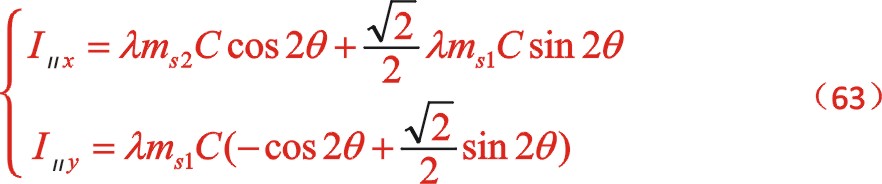
由上一篇文章75°的文中分析，顺反旋转时，角度“θ”用“— θ”代替，y方向也就是虚部的代数式“y”用“— y”代替这样的二原则，则式（63）与式（58）比较起来，同样适用这一原则。这可以检验运算过程的正确性，或者可能由于误输入加减符号导致的常识性错误。60°的二阶惯性力表达式也遵循这个，有兴趣的读者可以回看一下。
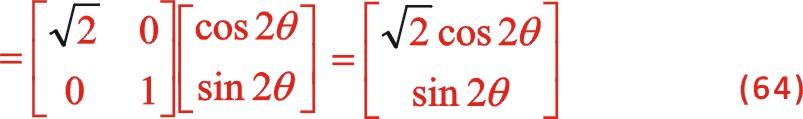
6.3用基础理论分析图12形式顺时针转动时惯性力
①一阶惯性力的计算
一阶惯性力合力的构成按图12所示的构成，依次写出如下
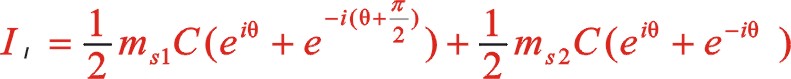
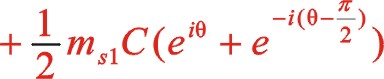
若两质量相等，则可以得出w型45°上述三种情形一阶惯性力的椭圆的短长轴之比为0.5。
②二阶惯性力的计算
二阶惯性力合力的构成按图12所示的构成，依次写出如下
垂直方向：
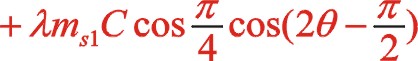
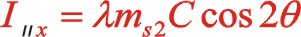
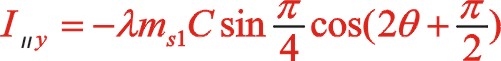
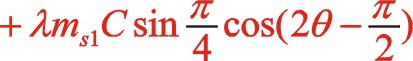
根据式（66），若两质量相等，可得出w型45°上述三种情形二阶惯性力的椭圆的短长轴之比为。
6.4图12与图10、图11利用坐标系旋转变换作出的公式的一致性推导
根据前述的理论，我们将图12的坐标系顺旋转方向转动45°后建立了新坐标系，也就是正角变换，这样一来该坐标系就与图10中一模一样。我们所做的事是已知式（65）的方程，利用该式怎样推导出式（56），以验算理论推导过程的一致性。我们进行坐标系的旋转变换，作如下
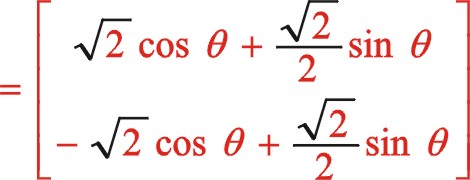
因为我们得到的式（56）是从偏置时开始计角度的，设重新建立新的坐标系后我们从偏置一边的活塞时开始计及角度α，则上面的“θ”用“ ”来代替，经运算后
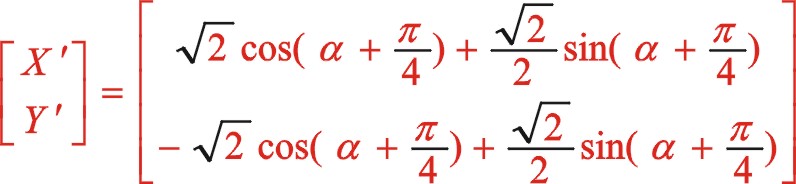
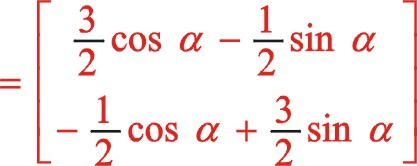
上式与式（56）一样，所以得证。
由于图12所画的转向是顺时针，为弄明白坐标系的旋转变换是正角变换还是负值变换，可以作图11的镜像图，所以得到是负角变换，因镜像后两图转向已一致所以式（65）保持不变，考虑到新坐标系的开始角的度量关系所以“θ”用“ ”来代替，推导如下：
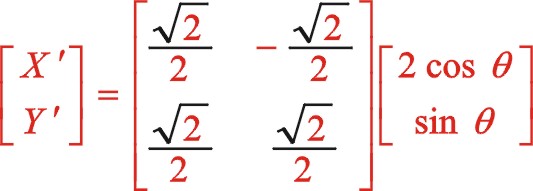
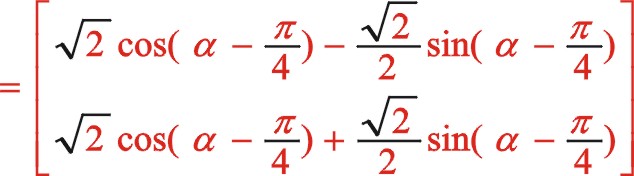
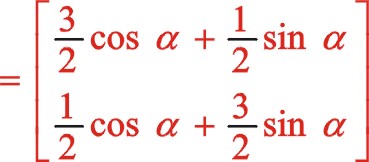
该式与式（61）保持一致，得证。
二阶惯性力的代数式（66）、（58）、（63）也能进行一致性推导。其它角度也行，此处不展开读者如若有兴趣自行推导。下面简单写出该角度的二阶惯性力推导方程式
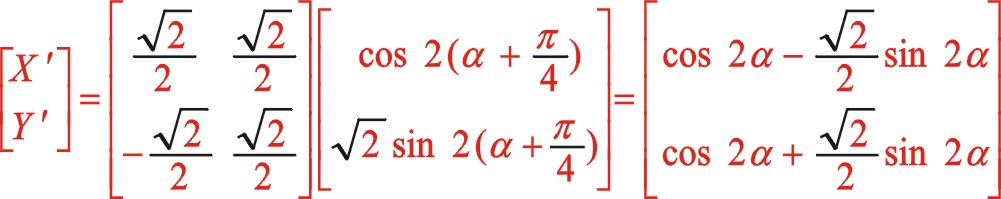
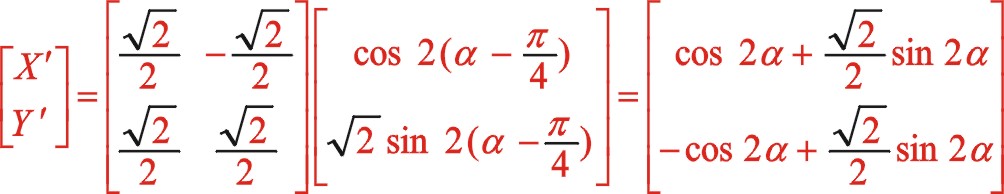
这种通过居中布置的参数方程推导出偏置时的参数方程，仅适用于ms2＝ms1时，对于二者质量不相等的情形，不能够通过坐标系的旋转变换来推导，因为研究的方法可灵活而固有的结构ms2不能够旋转，更多的理论——椭圆的小偏转理论、60°分布时椭圆大旋转理论——似乎也能支持该种算法。因此，还是用传统的方法计算各自的方程来得更直接些。
进行这些运算，可以加强理论的缜密性，可以检验推导过程的正确性，这些都是基于对数学中线性代数学科的研究、基于平时的善于发现，基于前述的基础理论中的正方向理论。
6.5总结
本处以安徽华晶机械有限公司生产的ww-0.9/10b-q型全无油二级为模版，假定气缸夹角为45°，计算其一、二阶往复惯性力。此处先假定三列往复质量相等，即ms为1.8kg，曲柄半径为0.0375m，曲柄半径连杆比λ为37.5/195，角速度ω为2π×(800/60)rad/s，现将上述结构参数分别代入上文中所列的相关公式中，运用计算机内excel程序列表、绘图计算分析，计算的结果绘制在上图的图10、图11、图12中，可以得到以下结论：
1）一阶惯性力由60°分布的圆变成椭圆，且椭圆的短长轴之比由1变成0.5，如果方向一致则是由1变成2；平均值由711n变成731n，有所增大；方向由跟随变成近似跟随。图10、11中已画出一、二阶惯性力刚开始时的矢量线，用椭圆断开表示，图12中反映一阶惯性力在某个时候有重合的可能。
2）二阶惯性力说明，其椭圆短长轴之比由0.333变成0.707。力的平均值由96.9n变成110.8n，有所增加。方向初看是乱的，但很有规律，因为三角函数是周期函数。这个规律待人们去认识、研究、发现、找寻合适的机构来平衡。
3）当ms2≠ms1时，60°分布一阶惯性力在ms2列方向形成椭圆的对称轴，而45°不是，说明角度优先于质量，说明w型时，60°分布是最优的。从式（9）的复数表达式、式（10）的几何表达式中可以看出，60°分布时一阶惯性力长短轴与角度无关，仅与质量有关，这与上也是吻合的。
4）它们的共同点是，曲柄转1周，一阶惯性力也转1周，且同向；二阶惯性力转2周，也同向。
若ms2≠ms1，会引起图10、图11、图12中两个椭圆有所歧化，或偏转，兼带扩压，使其相位、幅值有微量变化。
〈注：本文未完待续，更多精彩见下期！〉
参考文献
（1）宋瑞林，气缸夹角为60°的v6车用往复惯性力的平衡分析，[j]，汽车技术，1988.8
（2）李松虎，3w型往复惯性力的分析，[j]，压缩机技术，1987.3
（3）陆鹏程，张光胜，三星型压缩机振动问题研究，[j]，安徽工程科技学院学报，2009.1
（4）王再顺，夹角为90°的v型压缩机往复惯性力平衡的探讨，[j]，压缩机技术，1986.2
作者简介
陆鹏程，男，安徽桐城人，海军工程大学在职硕士毕业。现在中国人民解放军第四八一二工厂，安徽华晶机械有限公司工作，高级工程师。研究方向：压缩机研究与强度设计。
来源：本站原创
网友评论
条评论
最新评论